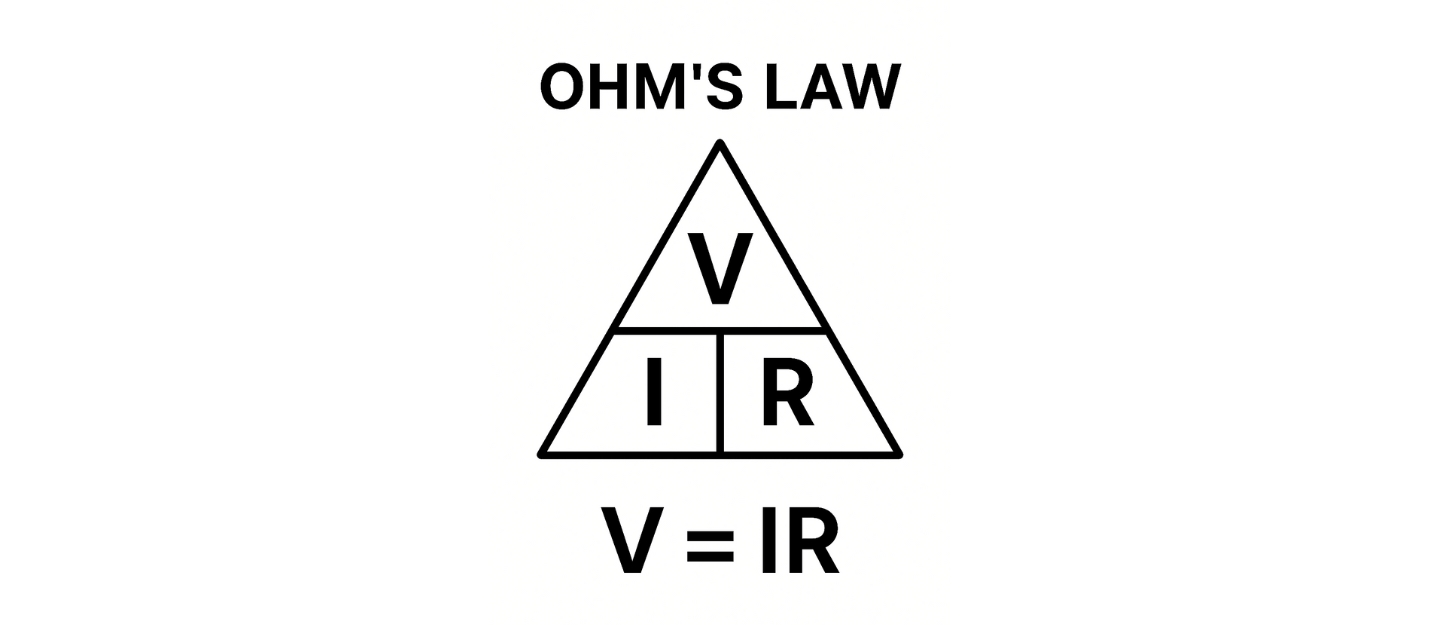
Ohm’s Law for ham operators is the foundation of all electrical and electronic work. It describes the simple yet powerful relationship between voltage, current, and resistance. Amateur radio operators rely on this law every time they design antennas, connect power supplies, or troubleshoot circuits.
It applies to every situation involving electricity, understanding Ohm’s Law helps ham operators build safer, more efficient, and more reliable stations.
The Basic Formula of Ohm’s Law
Ohm’s Law states that voltage equals current multiplied by resistance. Written as a formula, V = I × R. Voltage, measured in volts, represents the electrical pressure pushing electrons through a circuit.
Current, measured in amperes, describes the flow of electrons. Resistance, measured in ohms, represents the opposition to that flow. Furthermore, rearranging the formula allows you to solve for any one of the three values if the other two are known.
For example, if a circuit draws 2 amps of current through a 10-ohm resistor, the voltage across that resistor equals 20 volts. Conversely, if you know the voltage and resistance, you can calculate the current. Because of this flexibility, Ohm’s Law becomes a universal tool for problem-solving in ham radio.
Power and Ohm’s Law
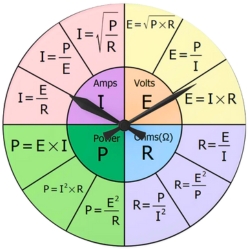
Beyond voltage, current, and resistance, power plays a major role in radio operation. Power, measured in watts, equals voltage multiplied by current. Written as P = V × I, this formula connects directly with Ohm’s Law.
By substitution, you can calculate power in terms of resistance or current as well. For instance, P = I² × R or P = V² ÷ R. Therefore, ham operators use Ohm’s Law and power formulas together to design circuits and predict performance.
Consider a transmitter that draws 10 amps from a 13.8-volt supply. Using P = V × I, the power equals 138 watts. If the station’s cabling has too much resistance, however, part of that energy wastes as heat instead of reaching the transmitter. This example highlights why Ohm’s Law is so important for maintaining efficiency.
Ohm’s Law in Power Supply Wiring
Ham operators often underestimate the importance of wire size. Every wire has resistance, and even small amounts reduce voltage at the equipment. For example, suppose your transceiver requires 20 amps at 13.8 volts.
If the supply cable has 0.05 ohms of total resistance, the voltage drop equals I × R = 20 × 0.05 = 1 volt. Consequently, your radio receives only 12.8 volts instead of 13.8, which may cause reduced output power or instability.
To prevent this, operators use larger gauge wires with lower resistance. Furthermore, keeping cable runs short reduces voltage drop. By applying Ohm’s Law, you can calculate the exact drop and ensure your radio operates at full efficiency.
Ohm’s Law in Antenna Systems
Antennas also demonstrate Ohm’s Law in action. Every antenna has an impedance, often around 50 ohms. When connected to a transmitter, the current and voltage at the feed point depend on the power level. For instance, a transmitter delivering 100 watts into a 50-ohm antenna produces a current of √(P ÷ R) = √(100 ÷ 50) = √2 ≈ 1.41 amps. The voltage at the feed point equals I × R = 1.41 × 50 ≈ 70.7 volts.
If the antenna’s impedance does not match the transmission line, reflections occur, causing standing waves and wasted power. Using Ohm’s Law, operators can understand these mismatches and apply tuners to correct them. Furthermore, by knowing expected current and voltage levels, hams can select coax and connectors that handle the load safely.
Ohm’s Law and Resistor Use in Circuits
Ham projects often include resistors to control current or divide voltage. For example, if you need 5 volts from a 12-volt supply, you can use a resistor divider. Suppose you choose two resistors, R1 = 3.5 kΩ and R2 = 5 kΩ.
The output voltage across R2 equals Vout = (R2 ÷ (R1 + R2)) × Vin. Substituting the values, Vout = (5000 ÷ 8500) × 12 ≈ 7.06 volts. If this output is too high, adjusting resistor values brings it closer to the desired voltage. Without Ohm’s Law, designing such circuits would be guesswork.
Heat and Ohm’s Law
Another practical example involves resistors and heat. Every resistor dissipates energy as power. If too much current flows, the resistor overheats and fails. For instance, a 100-ohm resistor with 20 volts across it carries I = V ÷ R = 20 ÷ 100 = 0.2 amps. Power equals V × I = 20 × 0.2 = 4 watts. If the resistor is rated for only 2 watts, it will overheat. Therefore, operators must calculate expected dissipation and select proper ratings.
Ohm’s Law in Safety Applications
Ohm’s Law also protects operators. Suppose you touch a live wire with 120 volts while your body presents 1,000 ohms of resistance.
Current equals V ÷ R = 120 ÷ 1000 = 0.12 amps, or 120 milliamps. Because currents above 100 milliamps can be fatal, this calculation shows why safety precautions matter.
Furthermore, insulation, fuses, and proper grounding reduce the risk of harmful currents.
Troubleshooting with Ohm’s Law
Ham operators frequently troubleshoot equipment by applying Ohm’s Law. If a transceiver draws more current than expected, the operator can calculate if a short circuit exists. For example, a 12-volt circuit with a measured resistance of 2 ohms should draw I = V ÷ R = 12 ÷ 2 = 6 amps.
If the actual draw is 12 amps, something is bypassing resistance, and the operator can investigate further. By comparing calculated and measured values, faults become easier to locate.
Ohm’s Law in Mobile Installations
Mobile installations highlight another application. A transceiver in a car connects to the battery through cables that run several feet. If those cables are too small, voltage drop reduces performance. For instance, with a current of 25 amps and cable resistance of 0.1 ohm, the voltage drop equals 2.5 volts.
As a result, the 13.8-volt supply delivers only 11.3 volts to the radio. This causes distortion or shutdown under load. Therefore, operators select larger cables and fuses to reduce resistance and maintain proper operation.
Conclusion
Ohm’s Law remains one of the most powerful tools for amateur radio operators. It explains the relationships among voltage, current, resistance, and power. Furthermore, it applies everywhere, from antenna design to mobile installations and from safety calculations to troubleshooting.
By mastering this simple law, ham operators ensure efficient stations, safer operations, and better performance. Ultimately, Ohm’s Law is not just theory; it is a practical guide that empowers every operator to understand, design, and improve their equipment with confidence.